Postingan Utama
- Get link
- X
- Other Apps
Soal dan Pembahasan Buku Sukino BAB 4 Polinomial LKS 8 Teorema Sisa Matematika Peminatan Kelas XI Kurikulum 2013
LKS 8
1. Jika f(x) dibagi (x+2) bersisa 14 dan dibagi (x-4) bersisa -4, maka f(x) dibagi (x^2-2x-8) bersisa....
A. -3x+8
B. 3x-8
C. 2x-4
D. 2x+4
E. 8x+3
Jawab : A
Pembahasan :
\(x + 2 = 0 \to x = - 2\)
f(x) dibagi (x+2)
\(x - 4 = 0 \to x = 4\)
f(x) dibagi (x-4)
Misal sisa pembagian f(x) oleh \({x^2} - 2x - 8\) adalah \(S\left( x \right) = mx + n\)
\({x^2} - 2x - 8 = 0\)
\(\left( {x - 4} \right)\left( {x + 2} \right) = 0\)
\(x = 4\) atau \(x = - 2\)
Dengan menggunakan teorema sisa \(f\left( a \right) = S\left( a \right)\)
Untuk \(x = 4 \to f\left( 4 \right) = S\left( 4 \right)\)\( \to - 4 = 4m + n....(1\)
Untuk \(x = - 2 \to f\left( { - 2} \right) = S\left( { - 2} \right)\)\( \to 14 = - 2m + n....(2\)
2. Suatu suku banyak f(x)
A. -3x+11
B. 3x-1
C. 5x-5
D. 5x+15
E. 10x-15
Jawab : B
Pembahasan :
\(x - 2 = 0 \to x = 2\)
\(\left( {x - 2} \right)\left( {x + 3} \right) = 0\)
\(x = 2\) atau \(x = - 3\)
Dengan menggunakan teorema sisa \(f\left( a \right) = S\left( a \right)\)
Untuk \(x = 2 \to f\left( 2 \right) = S\left( 2 \right)\)\( \to 5 = 2m + n....(1\)
Untuk \(x = - 3 \to f\left( { - 3} \right) = S\left( { - 3} \right)\)\( \to - 10 = - 3m + n....(2\)
Jadi, \(S\left( x \right) = 3x - 1\)
Jawab : D
Pembahasan :
P(x) dibagi oleh\[({x^2} - 2x)\]bersisa \(2x + 1\)
\({x^2} - 2x = 0 \to x\left( {x - 2} \right) = 0\)\( \to x = 0\) atau \(x = 2\)
Untuk \(x = 0\)\( \to P\left( 0 \right) = 2\left( 0 \right) + 1 \to P(0) = 1\)
Untuk \(x = 2 \to P\left( 2 \right) = 2\left( 2 \right) + 1 \to P\left( 2 \right) = 5\)
P(x) dibagi oleh \[({x^2} - 3x)\] bersisa \(5x + 2\)\( \to x = 0\) atau \(x = 3\)
Untuk \(x = 0 \to P\left( 0 \right) = 5\left( 0 \right) + 2\)\( \to P\left( 0 \right) = 2\)
Untuk \(x = 3 \to P\left( 3 \right) = 5\left( 3 \right) + 2 \to P\left( 3 \right) = 17\)
Misal sisa pembagian P(x) adalah \(S\left( x \right) = mx + n\)
\({x^2} - 5x + 6{\rm{}} = 0 \to \left( {x - 2} \right)\left( {x - 3} \right) = 0 \to x = 2\) atau \(x = 3\)
Dengan menggunakan teorema sisa \(P\left( a \right) = S\left( a \right)\)
Untuk \(x = 2 \to P\left( 2 \right) = S\left( 2 \right) \to 5 = 2m + n...(1\)
Untuk \(x = 3 \to P\left( 3 \right) = S\left( 3 \right) \to 17 = 3m + n...(2\)
Jadi, \(S\left( x \right) = 12x - 19\)
4. Diketahui R(x)=g(x).h(x).Jika g(x)
6. Jika suku banyak f(x)
f(x) dibagi (x-a)(x-b) dengan 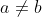 maka sisa pembagiannya adalah…
maka sisa pembagiannya adalah…
8. Jika polinom R(x)
adalah…
bersisa (5x-2)
Pembahasan Download di sini
Soal dan pembahasan LKS yang lain cek disini.
Kritik dan saran silahkan berikan di komentar, termasuk jika ada salah hitung dan salah ketik.
Terimakasih
Semoga bermanfaat 😊
1. Jika f(x) dibagi (x+2) bersisa 14 dan dibagi (x-4) bersisa -4, maka f(x) dibagi (x^2-2x-8) bersisa....
A. -3x+8
B. 3x-8
C. 2x-4
D. 2x+4
E. 8x+3
Jawab : A
Pembahasan :
\(x + 2 = 0 \to x = - 2\)
f(x) dibagi (x+2)
\(x - 4 = 0 \to x = 4\)
f(x) dibagi (x-4)
Misal sisa pembagian f(x) oleh \({x^2} - 2x - 8\)
\({x^2} - 2x - 8 = 0\)
\(\left( {x - 4} \right)\left( {x + 2} \right) = 0\)
\(x = 4\) atau \(x = - 2\)
Dengan menggunakan teorema sisa \(f\left( a \right) = S\left( a \right)\)
Untuk \(x = 4 \to f\left( 4 \right) = S\left( 4 \right)\)\( \to - 4 = 4m + n....(1\)
Untuk \(x = - 2 \to f\left( { - 2} \right) = S\left( { - 2} \right)\)\( \to 14 = - 2m + n....(2\)
Jadi, \(S\left( x \right) = - 3x + 8\)
A. -3x+11
B. 3x-1
C. 5x-5
D. 5x+15
E. 10x-15
Jawab : B
Pembahasan :
\(x - 2 = 0 \to x = 2\)
f(x) dibagi (x-2)
\(x + 3 = 0 \to x = - 3\)
f(x) dibagi (x+3)
Misal sisa pembagian f(x) oleh \({x^2} + x - 6\) adalah \(S\left( x \right) = mx + n\)
\({x^2} + x - 6 = 0\)\(\left( {x - 2} \right)\left( {x + 3} \right) = 0\)
\(x = 2\) atau \(x = - 3\)
Dengan menggunakan teorema sisa \(f\left( a \right) = S\left( a \right)\)
Untuk \(x = 2 \to f\left( 2 \right) = S\left( 2 \right)\)\( \to 5 = 2m + n....(1\)
Untuk \(x = - 3 \to f\left( { - 3} \right) = S\left( { - 3} \right)\)\( \to - 10 = - 3m + n....(2\)
Jadi, \(S\left( x \right) = 3x - 1\)
A. -22x+49
B. -12x+29
C. 12x+19
D. 12x-19
E. 22x-39
Jawab : D
Pembahasan :
P(x) dibagi oleh\[({x^2} - 2x)\]bersisa \(2x + 1\)
\({x^2} - 2x = 0 \to x\left( {x - 2} \right) = 0\)\( \to x = 0\) atau \(x = 2\)
Untuk \(x = 0\)\( \to P\left( 0 \right) = 2\left( 0 \right) + 1 \to P(0) = 1\)
Untuk \(x = 2 \to P\left( 2 \right) = 2\left( 2 \right) + 1 \to P\left( 2 \right) = 5\)
P(x) dibagi oleh \[({x^2} - 3x)\] bersisa \(5x + 2\)\( \to x = 0\) atau \(x = 3\)
Untuk \(x = 0 \to P\left( 0 \right) = 5\left( 0 \right) + 2\)\( \to P\left( 0 \right) = 2\)
Untuk \(x = 3 \to P\left( 3 \right) = 5\left( 3 \right) + 2 \to P\left( 3 \right) = 17\)
Misal sisa pembagian P(x)
\({x^2} - 5x + 6{\rm{}} = 0 \to \left( {x - 2} \right)\left( {x - 3} \right) = 0 \to x = 2\) atau \(x = 3\)
Dengan menggunakan teorema sisa \(P\left( a \right) = S\left( a \right)\)
Untuk \(x = 2 \to P\left( 2 \right) = S\left( 2 \right) \to 5 = 2m + n...(1\)
Untuk \(x = 3 \to P\left( 3 \right) = S\left( 3 \right) \to 17 = 3m + n...(2\)
Jadi, \(S\left( x \right) = 12x - 19\)
4. Diketahui R(x)=g(x).h(x).Jika g(x)
A. 16x-2
B. 2x-16
C. 2x+16
D. -2x+16
E. -16x+25. Diketahui suku banyak f(x)
A. 3x+17
B. 3x-17
C. 2x-5
D. -2x+5
E. -3x+17
6. Jika suku banyak f(x)
A. \(\frac{1}{2}{x^2} + 4x + 8\frac{1}{2}\)
B. \(\frac{1}{2}{x^2} + 4x - 8\frac{1}{2}\)
C. \(\frac{1}{2}{x^2} - 4x - 8\frac{1}{2}\)
D. \( - \frac{1}{2}{x^2} + 4x + 8\frac{1}{2}\)
E. \( - \frac{1}{2}{x^2} + 4x - 8\frac{1}{2}\)7. Jika suku banyak
A. \(\frac{{x - a}}{{a - b}}f\left( a \right) + \frac{{x - a}}{{b - a}}f(b)\)
B. \(\frac{{x - a}}{{a - b}}f\left( b \right) + \frac{{x - a}}{{b - a}}f\left( a \right)\)
C. \(\frac{{x - b}}{{a - b}}f\left( a \right) + \frac{{x - a}}{{b - a}}f\left( b \right)\)
D. \(\frac{{x - b}}{{a - b}}f\left( b \right) + \frac{{x - a}}{{b - a}}f\left( a \right)\)
E. \(\frac{{x - a}}{{b - a}}f\left( a \right) + \frac{{x - b}}{{a - b}}f\left( b \right)\)
8. Jika polinom R(x)
A. \(R\left( x \right) - \left( {x - \frac{b}{a}} \right)H\left( x \right)\)
B. \(R\left( x \right) + \left( {x - \frac{b}{a}} \right)H\left( x \right)\)
C. \(R\left( x \right) - \left( {ax - b} \right)H\left( x \right)\)
D. \(R\left( x \right) - \left( {bx - a} \right)H\left( x \right)\)
E. \(R\left( x \right) + \left( {ax - b} \right)H\left( x \right)\)9. Suku banyak P(x)
A. 4x^2+4x
B. 4x^2+4
C. x^2+4
D. x^2+4x
E. x^2+4x+410. Sisa pembagian suku banyak K(x)
A. (x-1)K(1)+(x-2)K(2)
B. (x-1)K(1)-(x-2)K(2)
C. (x-1)K(2)+(x-2)K(1)
D. (x-1)K(2)-(x-2)K(1)
E. (1-x)K(2)+(2-x)K(1)11. Suku banyak berderajat 3, jika dibagi (x^2-x-6)
A. x^3-2x^2+x+4
B. x^3-2x^2-x+4
C. x^3-2x^2-x-4
D. x^3-2x^2+4
E. x^3+2x^2-412. Jika suatu suku banyak p(x)=x^4+4x^3+6ax^2+4bx+c dibagi x^3+3x^2+9x+3
A. 2
B. 3
C. 5
D. 6
E. 813. Suatu suku banyak berderajat 3
A. x^3-2x^2+3x-4
B. x^3-2x^2+2x-4
C. x^3+2x^2-3x-7
D. 2x^3+2x^2-8x+7
E. 2x^3+4x^2-10x+914. Suatu suku banyak berderajat 3
A. -7
B. -5
C. -3
D. -1
E. 315. Suku banyak 3x^3+Ax^2+Bx+7
A. -6
B. -4
C. 0
D. 4
E. 6
Pembahasan Download di sini
Soal dan pembahasan LKS yang lain cek disini.
Kritik dan saran silahkan berikan di komentar, termasuk jika ada salah hitung dan salah ketik.
Terimakasih
Semoga bermanfaat 😊
- Get link
- X
- Other Apps
Labels:
BAB 4
Matematika Peminatan Kelas XI
Pembahasan Buku Matematika Peminatan
Pembahasan buku Sukino
polinomial
suku banyak
Comments
Popular Posts
Pembahasan Buku Sukino Kelas XI Matematika Peminatan revisi 2016
- Get link
- X
- Other Apps
[Lengkap] Kumpulan Soal dan Pembahasan Trigonometri Analitika
- Get link
- X
- Other Apps








Kok ga semuanya dibahas kak
ReplyDeletekak server 1 dan 2 gabisa dibuka "page not found" terus,tolong perbaiki
ReplyDeletekak server 1 dan 2 gabisa dibuka "page not found" terus,tolong perbaiki
ReplyDeletehay ber
Delete